【每日一题】Leetcode 1552. 两球之间的磁力
中等
数组
二分查找
排序
在代号为 C-137 的地球上,Rick 发现如果他将两个球放在他新发明的篮子里,它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子,第 i 个篮子的位置在 position[i] ,Morty 想把 m 个球放到这些篮子里,使得任意两球间 最小磁力 最大。
已知两个球如果分别位于 x 和 y ,那么它们之间的磁力为 |x - y| 。
给你一个整数数组 position 和一个整数 m ,请你返回最大化的最小磁力。
示例 1:
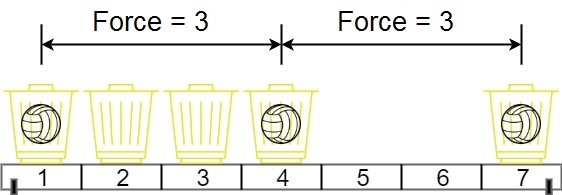
输入:position = [1,2,3,4,7], m = 3 输出:3 解释:将 3 个球分别放入位于 1,4 和 7 的三个篮子,两球间的磁力分别为 [3, 3, 6]。最小磁力为 3 。我们没办法让最小磁力大于 3 。
示例 2:
输入:position = [5,4,3,2,1,1000000000], m = 2 输出:999999999 解释:我们使用位于 1 和 1000000000 的篮子时最小磁力最大。
提示:
n == position.length 2 <= n <= 10^5 1 <= position[i] <= 10^9 所有 position 中的整数 互不相同 。 2 <= m <= position.length
思路:
- 最小磁力:对于 i < j < k 三个小球,最小磁力一定是 j−i 和 k−j 的较小值;
- 小球位置由算法确定,仅规定了放置小球数量为m个;
- 假设最大的最小磁力为ans,则小于ans的答案合法但不是最优,也就是磁力为[1, ans-1]合法但非最优,ans为合法最优,[ans+1, 最大磁力]的放置方法为不合法(这是因为规定了放置小球数量,如果大于ans,则放置小球数量将小于m个)。
- 所以可以对在[1, 最大磁力]的范围内查找ans,而根据思路3可以使用二分查找,则设区间为[left, right],每次查找left+right的平均值mid,则有:
当mid合法,则缩小左边界left,即 ans = mid, left = mid + 1;(依据思路3,ans左侧的[1, ans-1]都为非最优,所以查询mid右侧即缩小左边界)
当mid不合法,则缩小右边界right,即 right = mid - 1(依据思路3,ans右侧的[ans + 1, 最大磁力]都不合法,所以排除mid右侧即缩小右边界) - 如何判断当前ans是否合法:二分查找[1, 最大磁力]列表,设当前磁力值为x,根据贪心原则从排序后的position列表第一位开始,依次相隔x距离放置小球,若放置小球数量大于m则当前磁力x合法。
代码:
class Solution:
def maxDistance(self, position: List[int], m: int) -> int:
def check(x: int) -> bool:
"""
检查当前磁力值是否合法
param x: 当前查询的磁力值
return : 返回当前查询的磁力值是否合法,即放入的小球数量是否大于等于m
"""
pre = position[0] # 根据贪心原则,从第一位开始放置
cnt = 1 # 在当前磁力值下,能够放置的小球数量
for i in range(1, len(position)):
if position[i] - pre >= x: # 判断当前位置与上一个放置小球的位置之间是否相隔 x
pre = position[i] # 更新最新放置小球的位置
cnt += 1
return cnt >= m
position.sort() # position排序 从小到大
"""
依据[1, 最大磁力] 设定开始和末尾指针
"""
left, right, ans = 1, position[-1] - position[0], -1
while left <= right:
mid = (left + right) // 2;
if check(mid):
"""
当前磁力值 mid 合法,记录为ans并缩小左边界
"""
ans = mid
left = mid + 1
else:
right = mid - 1 # mid不合法,缩小右边界
return ans
感谢浏览,欢迎关注祁彧w博客!
文章评论