Opening the black box of Deep Neural Networks via Information

本文部分内容待优化重写

引言

互信息(Mutual Information)：是信息论里一种有用的信息度量，它可以看成是一个随机变量中包含的关于另一个随机变量的信息量，或者说是一个随机变量由于已知另一个随机变量而减少的不肯定性，由\(I(X;Y)\)表示。

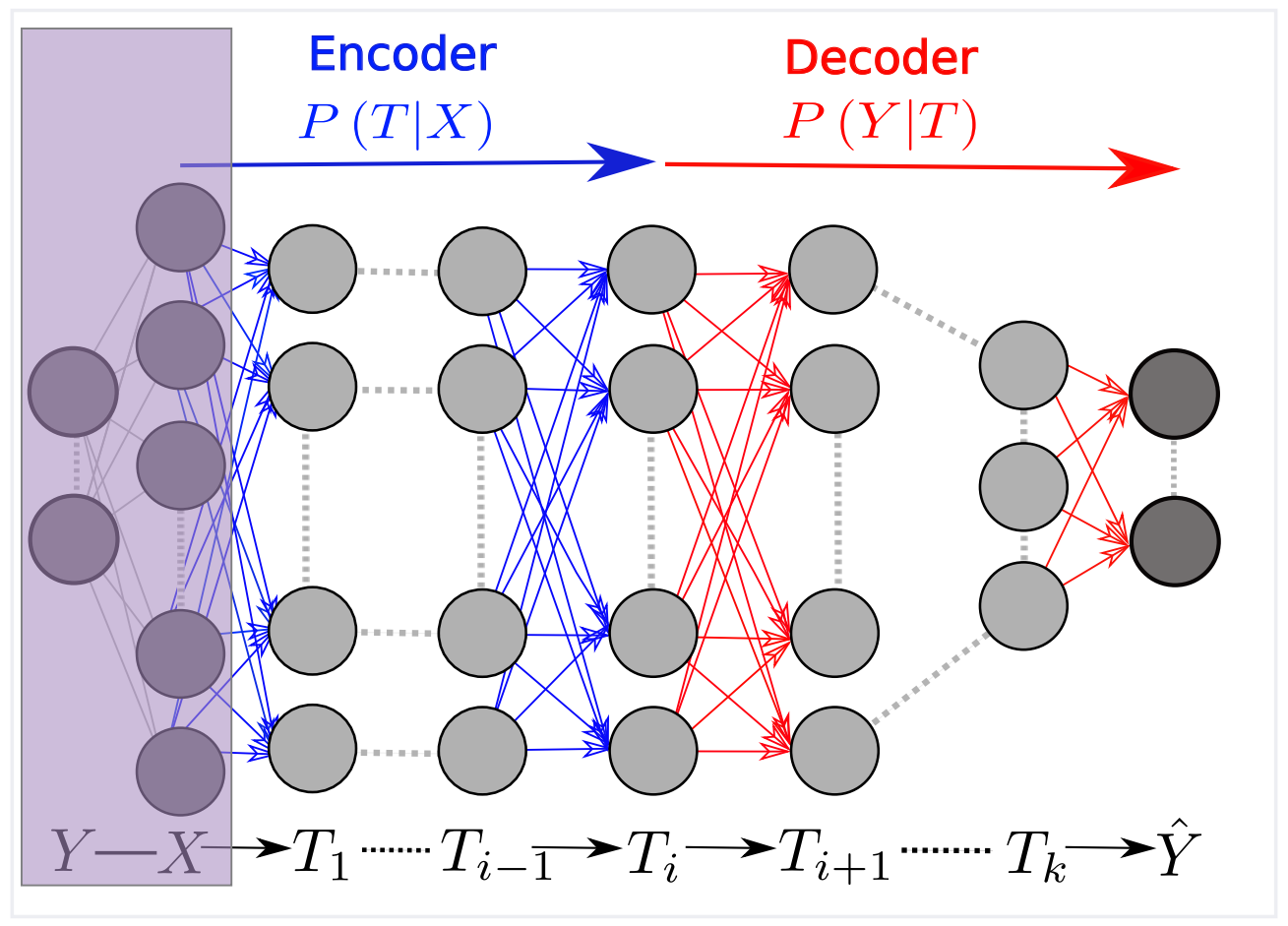
如上图所示，是一个完整的DNN内部层关于输入X的马尔科夫链。其中，任何一个输入的表示T，通过编码定义为\(P(T|X)\)，通过解码定义为\(P(\hat{Y}|T)\)，同时可以通过其信息平面坐标进行量化：\(I_{X}=I(X;T)\)以及\(I_{Y}=I(T;Y)\)。对于给定的互信息，在期望输出Y上，信息瓶颈边界表达(characterizes)表示了最大程度压缩输入X的最优表示(representation)。在训练之后，当X输入网络时，信息通过层层处理，即马尔科夫链，最终能够得到预测值\(\hat{Y}\)。并且，\(I(Y;\hat{Y})/I(X;Y)\)可以量化网络捕获的相关信息量。

Abstract

尽管人们对于DNN取得了巨大的成功，但对于深度神经网络（DNN）或其内部组织的学习仍然没有全面的理论理解。先前的工作[Tishby and Zaslavsky(2015)]提出，在信息平面(Information Plane)上分析DNNs，即每个层在输入和输出变量上保留的互信息值的平面。所以，他们建议网络的目标是优化每一层的压缩和预测之间的信息瓶颈(Information Bottleneck (IB))的tradeoff。

在这项工作中，我们跟进了这一想法，并证明了DNN信息平面可视化的有效性。我们有以下主要结果：

• 在标准DL中，大多数训练阶段都花在将输入压缩为有效表示(representation)上，而不是在拟合训练标签上。
• 表示压缩阶段开始于训练误差变小时，并且随机梯度下降（SGD）阶段从快速移动到较小的训练误差，转变为受训练误差值约束的随机松弛(stochastic relaxation)或随机扩散(random diffusion)。
• 收敛层位于或非常接近于信息瓶颈（IB）的理论边界，从输入到任何隐藏层以及从该隐藏层到输出的映射满足IB自洽方程。这种通过噪声机制的泛化是深层神经网络所独有的，在单层网络中是不存在的。
• 当添加更多隐藏层时，训练时间会显著缩短。因此，隐藏层的主要优点是计算性。这可以通过被减少的松弛时间来解释，因为它与前一层的信息压缩成超线性（对于简单的扩散是指数级的）。
• 当我们预计IB曲线上相变附近的随机松弛会出现临界放缓时，我们预计隐藏层会收敛到这样的临界点。

Method

首先，将整个隐藏层视为单个随机变量T，并且通过编码器表示为\(P(T|X)\)，通过解码器表示为\(P(Y|X)\)分布，之后由于我们只对流经网络的信息感兴趣，所以表示(representation)的可逆变换可以保留信息及生成等效的表示，即使单个神经元编码的输入特征完全不同。

然后，我们可以通过使用两个数字或是顺序参数来量化表示，并且它们对于T的可逆重参数以及T与输入X和期望输出Y的互信息都是不变的。

最后，我们通过比较各层与信息论中的最优表示，来量化各层的质量，然后描述深度学习SGD如何实现这些最优表示。

互信息 Mutual Information

给定两个随机变量X和Y，以及一个联合分布p(x,y)，则X和Y之间的互信息可以表示为：

其中，\(D_{KL}[p||q]\)表示分布p和q的库尔贝克-利布勒(Kullback-Liebler)散度，\(H(X)\)和\(H(X|Y)\)分别是X的熵和Y的条件熵。
互信息平均量化了输入变量X包含的关于标签Y的相关位(relevant bits)的数量。

在DNNs中，互信息的两个性质非常重要：
1、第一个是他对可逆变换的不变性
$$I(X;Y)=I(\psi(X);\phi(Y))，\psi和\phi分别是两个可逆函数$$
2、数据处理不等式(Data Processing Inequality (DPI))：在马尔科夫链上，对于任意3个变量\(X\rightarrow Y\rightarrow Z\)
$$I(X;Y)\geq I(X;Z)$$

信息平面

任何表示(representation)的变量T，都是输入X的一个(或随机)的映射，并且其可以表示为关于X和Y的联合分布，或者是通过编码和解码的P(T|X)和P(Y|T)的分布。若给定一个P(X;Y)，则T以坐标\((I(X;T),I(T;Y))\)唯一的映射到信息平面上的一个点。
当其应用于具有K第i层DNN上的马尔科夫链时，\(T_{i}\)是一个单个多元变量，其表示个隐藏层，同时这些层被映射到平面中的K个单调连接点上——此后是唯一的信息路径——满足以下DPI链：

$$I(X;Y)\geq I(T_{1}\;Y)\geq I(T_{2};Y)\geq...\geq I(T_{k};Y)\geq I(\hat{Y};Y)$$

$$H(X)\ge I(X;T_{1})\ge I(X;T_{2})\ge...\ge I(X;T_{k})\ge I(X;\hat{Y})$$

信息瓶颈的最优表示

那么X或是Y的最优表示的特征是什么？对于最优表示，最小充分统计(minimal sufficient statistics)是一个很好的选择。

在这里，充分统计是X及S(X)的映射或是隔断(partitions)，其能够捕捉X上所有关于Y的信息。即\(I(S(X);Y)=I(X;Y)\)。那么，最小充分统计T(X)可以通过马尔科夫链表达为\(Y\to X\to S(X)\to T(X)\)，然后可以使用DPI将其转化为约束优化问题：

$$T(X)=arg\underset{S(X):I(S(X);Y)=I(X;Y)}{min}I(S(X);X)$$

若将将t∈T定义为x∈X的压缩表示，那么x的表示现在由映射\(p(t|x)\)定义。则对\(Y\rightarrow X\rightarrow T\)的马尔科夫链有：

在信息平面中可视化DNNs

使用两个线性参数\(I(T;X)\)以及\(I(T;Y)\)，可视化并比较不同的网络架构在\(P(X;Y)\)中保存相关信息的效率。

Result

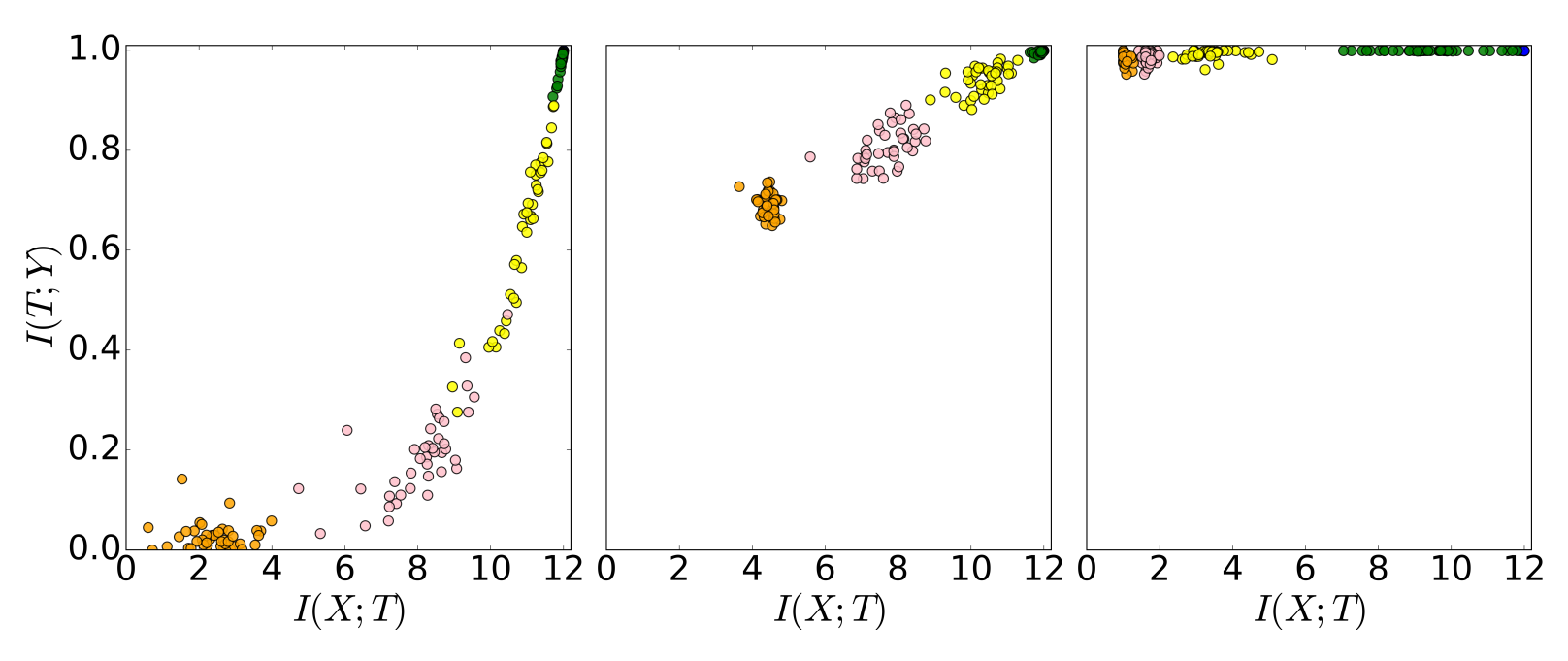
上图显示了在信息平面中SGD优化过程中的50个随机网络的层，其中相同颜色的点表示网络中同一层的不同权重，共四种颜色则表示网络中的四个隐藏层并且每个隐藏层共有50种不同的权重。左图为网络初始权重，中间图为在400个epoch时，右图为9000个epoch之后。

其中，横轴代表隐藏层表示T对输入X的压缩率，压缩率越高隐藏层T所含输入X的信息越少(I(X;T)越小)，即隐藏层越深。纵轴代表隐藏层表示T中关于预测Y的相关信息，越接近于1则失真越小。

由图可以知道，在训练过程中，隐藏层表示T中关于预测Y的互信息，在训练初始时，浅层比深层的互信息量更多，但随着训练增多，各层的关于预测Y的互信息量逐渐增多，直至1。

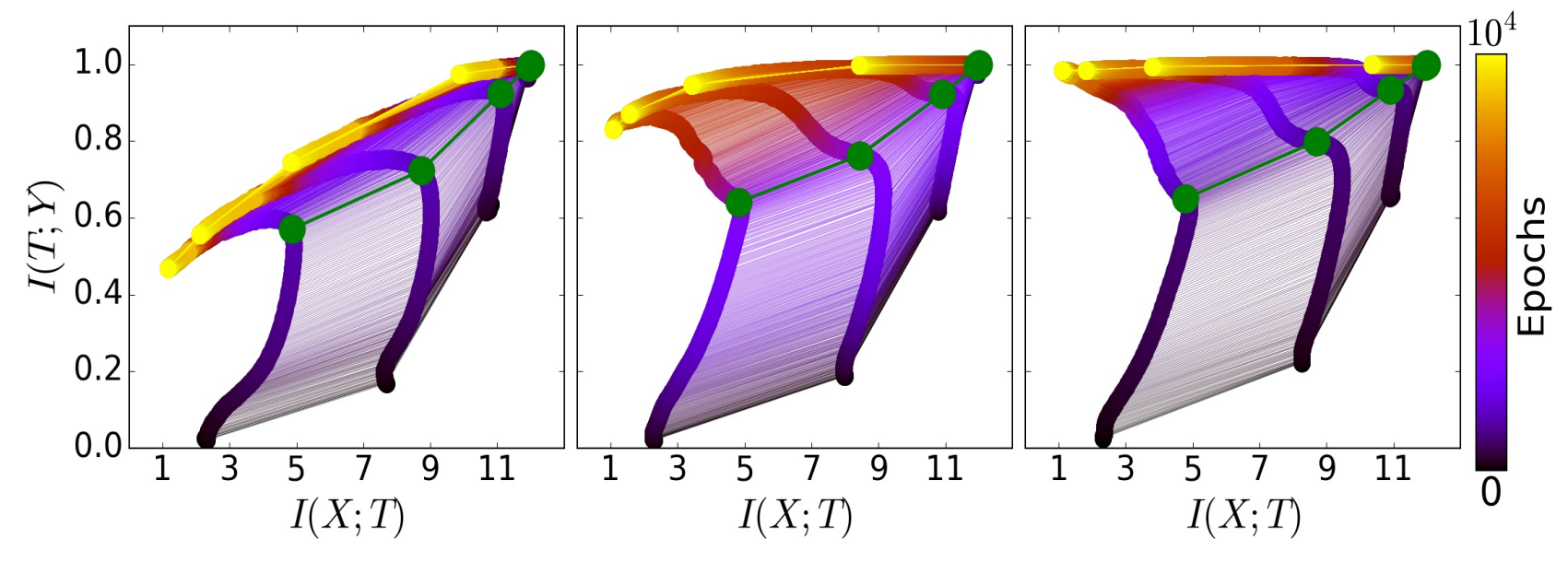
上图显示了在信息平面中，对于不同训练数据量，同一网络的各层，其中粗线表示了网络中一层的变化情况，细线表示同一网络各层之间的连接，绿点及绿线表示了两个优化阶段的分界线。左图为使用5%的数据量训练，中间图为使用45%的数据量训练，右图为使用85%的数据量训练。

由该图可知，网络中的浅层始终对输入X有较高的互信息以及对标签Y失真度很小。同时，在网络训练中，两个优化阶段在图中清晰可见(绿色分界线)，第一个阶段-快速ERM阶段，该阶段保持在较小的epoch范围内(几百epoch)，在该阶段中隐藏层提高对标签Y的信息量，同时保持DPI顺序(层与层之间，浅层具有更高的信息量，注：见信息平面)，第二个阶段，具有更长的训练时间，且该阶段隐藏层对输入X的信息量在减少，隐藏层丢失对于标签Y的不相关信息，直至收敛(到黄点)，将该阶段称之为表示压缩阶段(representation compression phase)。

在小样本5%和大样本85%中，ERM阶段很相似，但是对于表示压缩阶段，小样本出现隐藏层对于标签Y的信息量显著减少的情况，但在大样本中标签Y的信息量大部分在增加，这种情况可以归结于在小样本中出现过度拟合的情况，但其可以通过早期停止方法(early stopping methods)避免。所以，过度拟合可以看做是在表示压缩阶段，在简化对于输入X的信息量(即简化隐藏层的表示)的同时，也丢失了对于标签Y的相关信息。

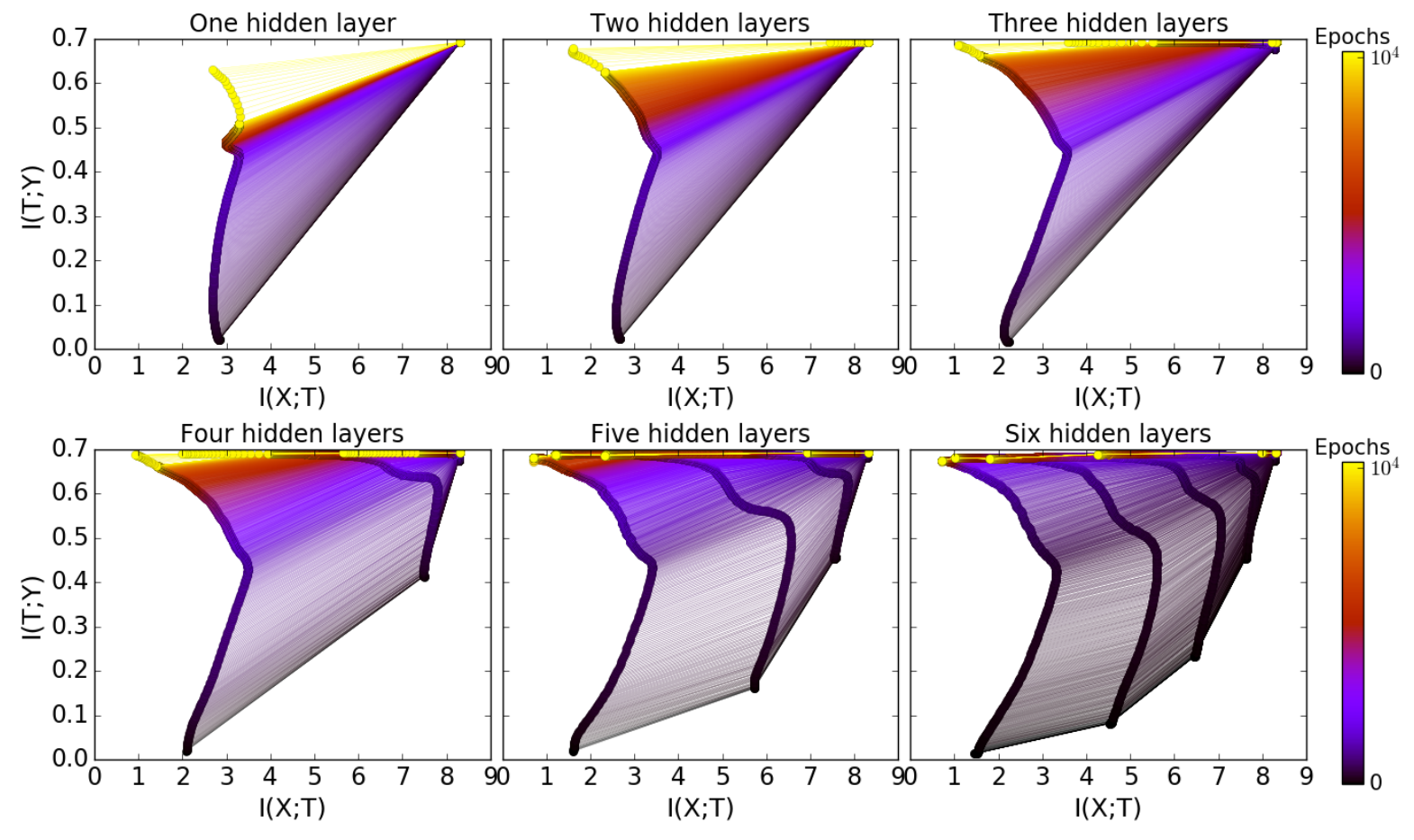
上图显示了作者在增加隐藏层之后的计算效益。图中从左至右从上至下分别显示了1~6个隐藏层中在信息平面中的可视化，并且随着隐藏层数量的递增，其各层内部的神经元递减，从初始的12个神经元，通过每层2个递减，到最后一层只有2个神经元。

作者发现几个结论：

• 添加隐藏层可以显著减少训练次数，从而实现良好的泛化。
• 每个隐藏层，其压缩阶段的训练次数，都比上一个隐藏层的压缩阶段训练次数短。
• 对于更深(神经元更少、更接近输出)的隐藏层，其压缩阶段的速度越快。
• 即使是很宽(神经元很多)的隐藏层最终也会在传播(diffusion)阶段压缩。增加额外的宽度(增加神经元)没有帮助。

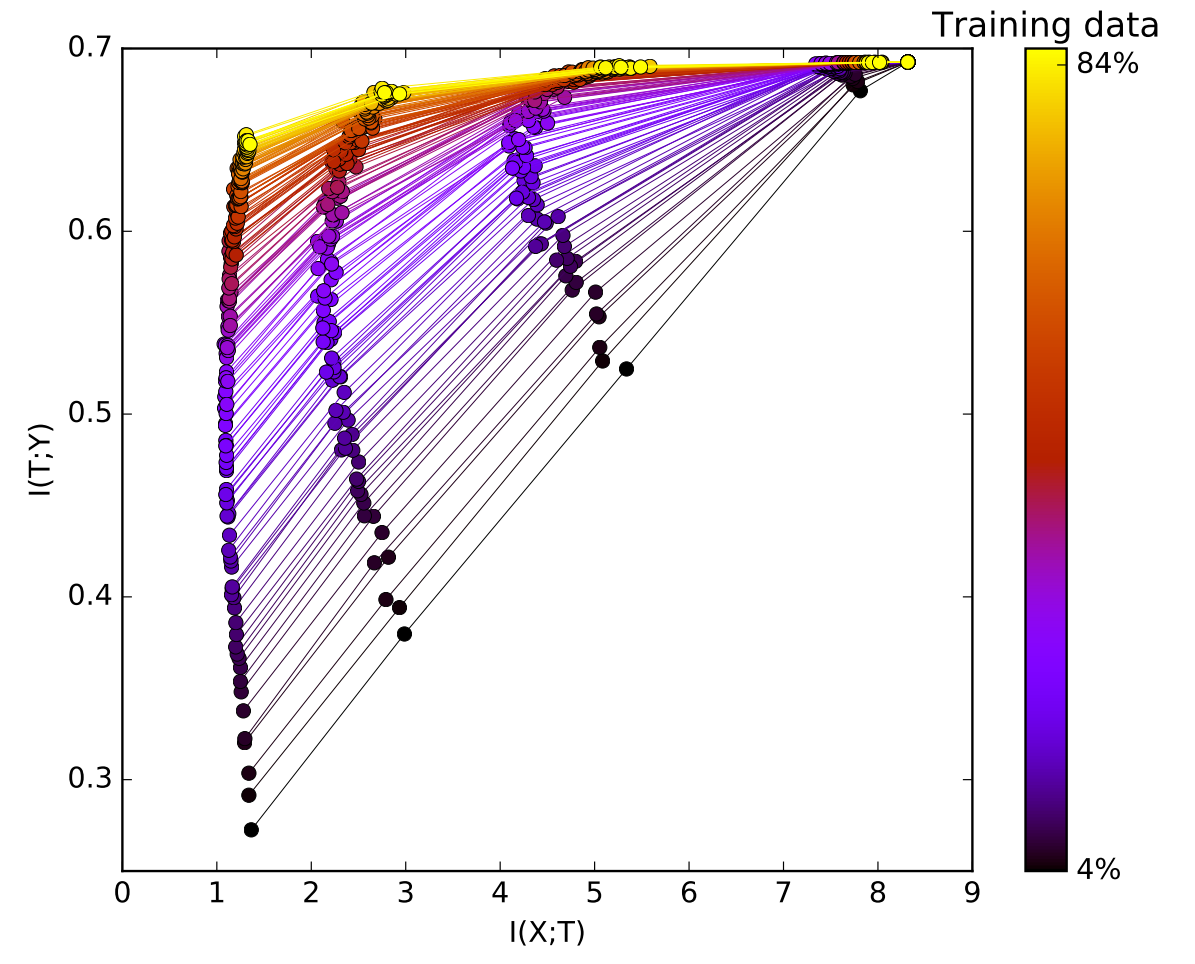
上图显示了再同一网络中，对于不同数据量网络训练时在信息平面中的可视化结果。其中每一条点-线段代表一个规模的数据量在该网络下的信息平面可视化结果。

可以看到，对于不同数据量，每一隐藏层对于输入X的信息量基本是不变的，但是对于标签Y的信息量，数据量越多其携带标签Y的信息量越多。

总结

本文基于互信息，在前人的基础上对DNNs在信息平面上进行了可视化，以便更好地理解深度学习（DL）中的训练动态、学习过程和内部表征。

1、每个隐藏层的训练过程可分为两个阶段，第一个阶段为“学习”，主要学习输入X的信息，这占训练过程的一小部分，第二个阶段为“压缩”，主要通过压缩输入X的信息，去除不含有标签Y的信息，使得该层的表示，含有较少的输入X的信息，较多的标签Y的信息，并且该阶段占训练过程的大部分时间。

2、在训练开始时，网络中的隐藏层根据所在深度，其包含的输入X的信息量是不同且递减的，并且添加隐藏层可以实现更好的泛化，并且减少训练次数。

3、过度拟合可以看做是在表示压缩阶段，在简化对于输入X的信息量(即简化隐藏层的表示)的同时，丢失了对于标签Y的相关信息。

4、对于不同数据量，每一隐藏层对于输入X的信息量基本是不变的，但是对于标签Y的信息量，数据量越多其携带标签Y的信息量越多。

但是，本文的实验是基于一个全连接的神经网络，完全服务于实验及数据，能够比较容易计算出互信息。所以对于其他网络结构来说，互信息可能并不容易。

博客CSDN链接：【论文学习】Opening the black box of Deep Neural Networks via Information

感谢浏览，欢迎关注祁彧w博客！